
Perché ingrasso?
23 Giugno 2018
Quanti caffè al giorno possiamo bere?
29 Giugno 2018Che cos’è il paradosso di Simpson e come possiamo prevenirlo? La statistica a volte necessita di alcune accortezze. Scopriamo in questo articolo uno dei paradossi più famosi.
Paradosso di Simpson
Vi piacerebbe che l’articolo di oggi fosse dedicato all’Homer più importante della storia dei cartoni. Oggi però non parliamo di lui, ma di E.H. Simpson che descrisse nel 1951 un paradosso presente in statistica e menzionato sulla rivista Journal of the Royal Statistical Society.
Che cos’è il paradosso di Simpson?
È un paradosso statistico dove è possibile che si verifichino conclusioni tra loro discordanti. Questo a causa della raccolta dati e alla divisione dei gruppi nella condizione di partenza.
Un esempio per comprenderlo
Sappiamo tutti che uno dei più amati personaggi dei cartoni animati, Homer Simpson, è un gran mangiatore di ciambelle. Prenderemo proprio lui come tester e dimostreremo come la statistica possa ingannare, se non teniamo conto di alcune variabili.
Gli chiederemo ad Homer di pescare da 4 cesti. Questi 4 cesti sono pieni di ciambelle di due tipologie: ciambelle dalla glassa viola e ciambelle dalla glassa bianca.
Lui vuole mangiare quelle dalla glassa viola e non quelle dalla glassa bianca.
Il dettaglio fondamentale è che questi quattro cesti sono a coppie e Homer potrà scegliere un solo cesto per ciascuna coppia.
Perciò per farlo gli daremo la possibilità di scegliere solo da due cesti su quattro. Gli basterà selezionare il cesto che in percentuale contenga un maggior numero di ciambelle con la glassa da lui desiderata.
Per farlo gli diremo la verità di come abbiamo distribuito le ciambelle:
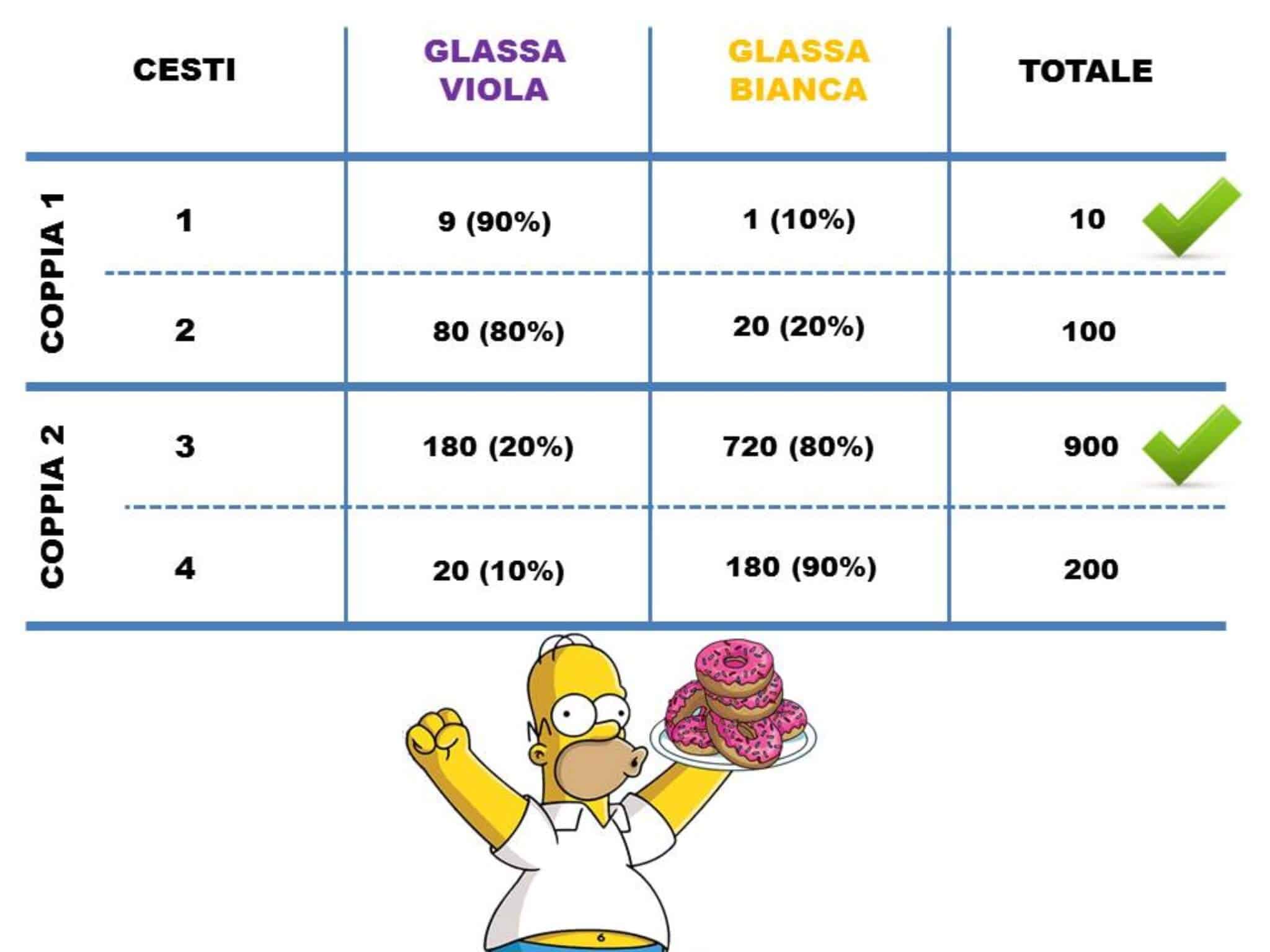
COPPIA n.1
- Cesto 1: 10 ciambelle di cui solo 1 ha la glassa bianca (9 su 10 hanno la glassa viola);
- Cesto 2: 100 ciambelle di cui solo 20 hanno la glassa bianca (80 su 100 hanno la glassa viola).
COPPIA n.2
- Cesto 1: 900 ciambelle di cui 720 hanno la glassa bianca (180 su 900 hanno la glassa viola);
- Cesto 2: 200 ciambelle di cui 180 hanno la glassa bianca (20 su 200 ha la glassa viola).
La seconda coppia di cesti ha una maggioranza di ciambelle a glassa bianca. Ma per il povero Homer sarà più difficile pescare la ciambella di suo interesse!
Ma procediamo con ordine.
Da quali due cesti pescherà Homer?
Qui le cose sono semplici perché basterà vedere dove Homer ha più probabilità di pescare una ciambella dalla glassa viola.
Nel primo gruppo di cesti gli converrà pescare dal cesto 1.
Questo perché avrà il 90% di probabilità di pescare la ciambella di suo piacimento, rispetto all’80% del secondo cesto.
Nel secondo gruppo di cesti gli converrà pescare anche in questo caso dal cesto 1 (in immagine cesto 3), in quanto c’è il 20% di probabilità di pescare la ciambella di suo interesse, a fronte del 10% del cesto n.4!
L’immagine sottostante rende più chiaro il tutto.
Il paradosso di Simpson: quando si verifica?
Adesso che Homer ha selezionato i due cesti di suo interesse. Cosa ha fatto riassumendo? Ha selezionato dove ha più probabilità di avere le sue ciambelle preferite. Ora mettiamo insieme il cesto del gruppo 1 con la più alta percentuale di ciambelle con glassa viola, con il cesto n.3.
Facciamo la stessa cosa con gli altri due cesti con più alta percentuale di ciambelle a glassa bianca (cesto n.2 e cesto n.4).
Ora chiediamo a Homer di pescare dai due cesti quello dove ha più probabilità di guadagnarsi un’altra ciambella di suo interesse. Lui l’ha trovato talmente scontato come ragionamento che seleziona il cesto 5 in immagine e…SBAGLIA.
E la soluzione è perché sono cambiate le carte in tavola.
Si è verificato il paradosso di Simpson. Ecco perché!
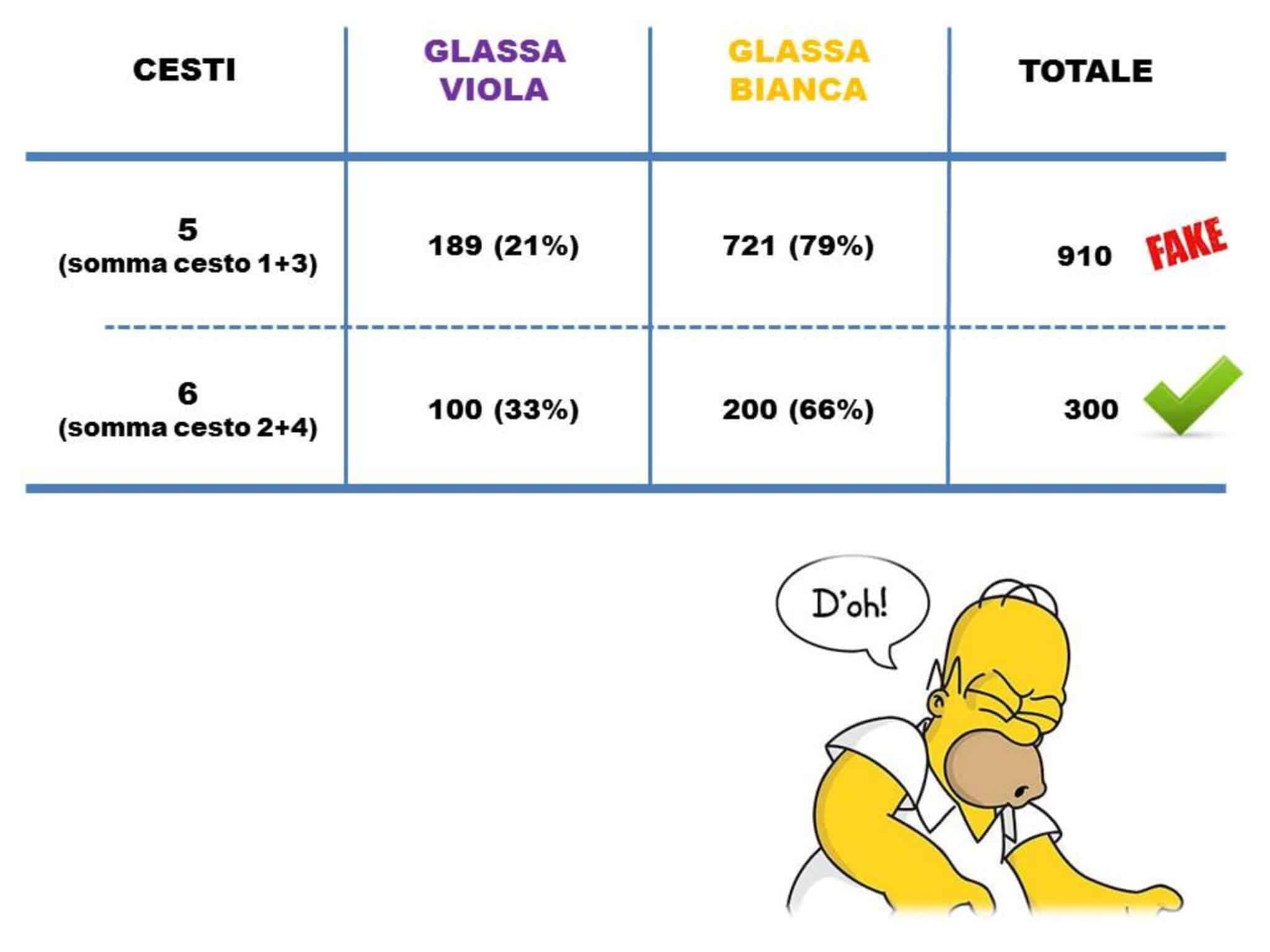
Sommando i due cesti si è verificato un problema. Le percentuali ora sono diverse.
Perché?
Quando si verifica questo paradosso in statistica è perché non abbiamo tenuto conto di come sono stati creati i gruppi. Al posto delle ciambelle avremmo potuto usare dei pazienti sotto sperimentazione farmacologica.
I risultati sarebbero stati contraddittori e poco chiari.
Come evitare che si verifichi il paradosso di Simpson?
È importante che le percentuali di casi nei gruppi siano uguali e non entrino in gioco variabili distorcenti.
Questo, come ben intuibile, non è cosa semplice in una sperimentazione scientifica.
Le variabili che entrano in gioco sono spesso confondenti sul risultato. Questo appena visto ne è un tipico esempio.
Sei in cerca di un nutrizionista a Torino o di un nutrizionista a Milano?
Ti piace la ricerca scientifica e vuoi leggere una guida gratuita su come interpretare gli studi scientifici?

